TL;DR
A computer science student converted a supermarket floorplan into a grid, wrote a C++ path optimizer using simulated annealing and 2-opt moves, and found the shortest route was unusable in practice because it created too many sharp turns. Adding a penalty for turns produced smoother, more human-friendly paths and highlighted the bigger problem of optimizing the wrong metric.
What happened
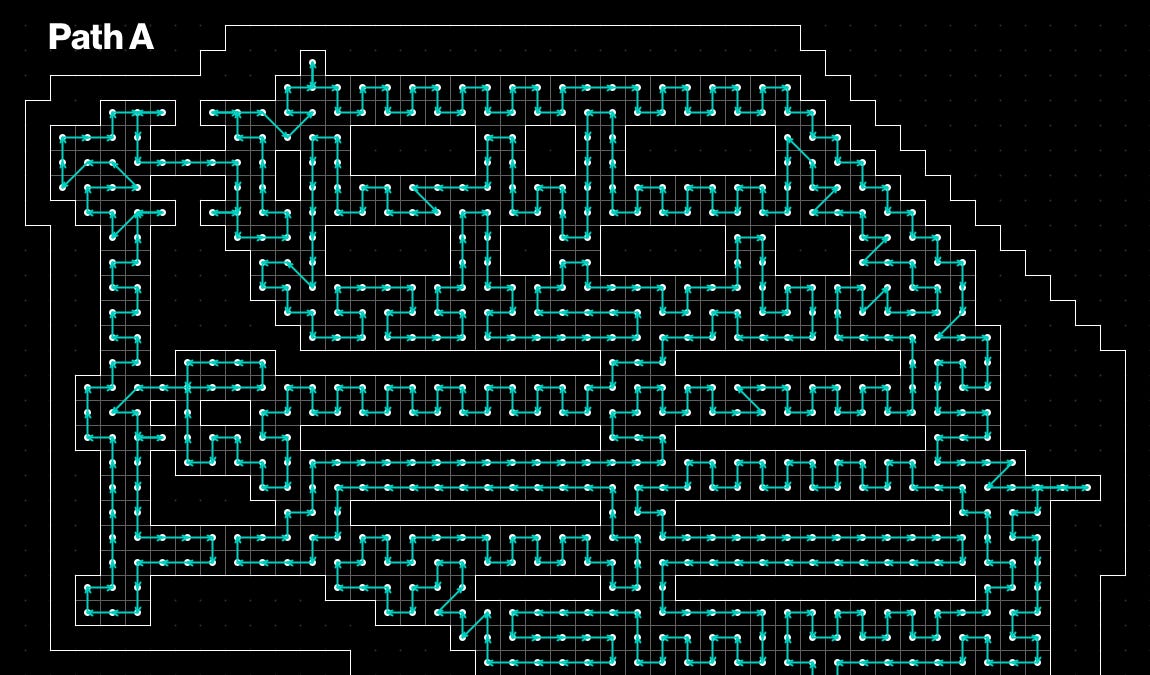
A student tasked with sweeping a supermarket turned the store layout into a tiled grid and built a visual editor in Processing to map the space. Each tile became a node in a graph that allowed horizontal, vertical and diagonal moves. Facing a computationally hard routing problem (linked to the Traveling Salesman Problem), they implemented a C++ optimizer that used simulated annealing and repeated 2-opt local moves to improve candidate routes. The first output minimized distance but produced a path with many abrupt turns that would be impractical for a human sweeper. To address this, the author modified the cost function to add a penalty for sharp turns, yielding smoother but slightly longer routes. The author also provided an adjustable penalty 'slider' to trade distance for smoothness, and reflects on how optimizing for easy-to-measure metrics can produce undesirable real-world outcomes. The optimized route was not used on the job; the author swept normally.
Why it matters
- Choosing the wrong objective (cost function) makes technically correct solutions practically useless.
- Small modeling choices—like whether to penalize turns—change outcomes significantly for human tasks.
- This example generalizes to digital systems: optimizing simple metrics (engagement, watch time) can harm users.
- Designers and engineers need to incorporate real-world constraints, not just mathematically convenient ones.
Key facts
- Author is a Computer Science student who took on a supermarket sweeping task.
- The store floorplan was converted into a grid; tiles were classified as sweepable or obstacles.
- A visual editor was built in Processing to map the floor and export the graph.
- Movement allowed horizontal, vertical and diagonal moves between adjacent tiles.
- The optimization problem was framed like the Traveling Salesman Problem.
- The optimizer was implemented in C++ and used simulated annealing as the heuristic.
- Local changes used the 2-opt move: remove two edges and reconnect them differently.
- Initial optimized path minimized distance but produced many sharp turns and was impractical.
- Adding a turn-angle penalty to the cost function produced smoother, more walkable routes.
- The author did not use the optimized route while doing the actual sweeping.
What to watch next
- How designers and product teams define cost functions for real-world tasks—this article shows the stakes.
- Whether retailers or facilities teams adopt route-penalty optimizers in operations: not confirmed in the source.
- Regulatory or industry responses to algorithmic systems that optimize harmful metrics (engagement, watch time): not confirmed in the source.
Quick glossary
- Simulated annealing: A heuristic optimization method that probabilistically accepts changes early on to escape local minima, then gradually becomes more selective to converge on a good solution.
- 2-opt move: A local operation for routing problems that removes two edges from a tour and reconnects the segments differently to try to shorten the path.
- Cost function: A formula used by an optimizer that assigns a numeric score to a candidate solution; optimization minimizes or maximizes that score.
- Graph (network): A data structure of nodes connected by edges used to represent relationships or paths, such as tiles connected to neighboring tiles on a floorplan.
- Traveling Salesman Problem (TSP): A classic computational problem that asks for the shortest possible route visiting every node exactly once; finding the exact solution is computationally hard for large graphs.
Reader FAQ
Did the author use the optimized path when actually sweeping?
No — the author says they swept the floor like a normal person and did not use the optimized path.
What optimization algorithm was used?
Simulated annealing with 2-opt local moves, implemented in C++.
Is the code available?
Yes — the source article includes a link to a GitHub repository with the code.
Did the optimizer make sweeping faster in practice?
Not confirmed in the source.
Discover more from The Debug Lab Public experiments in fixing what’s broken: from slow algorithms to fractured attention. For problem solvers ready to optimize their code and life. Subscribe By…
Sources
- I got paid minimum wage to solve an impossible problem
- Long Treated as Volunteers, Tips-Only Supermarket …
- – THE NEXT FARM BILL
- Solve The Outbreak – 508 Accessible Version
Related posts
- 5 Google Photos features that have no good open source app alternative (yet)
- CES 2026 Sees Few New Cars as Automotive Focus Shifts to China
- How to Build a Claude-like Coding Agent in Around 200 Lines of Python